python kruskal算法解决最小生成树问题

最小生成树是无向图论中很常见的一个问题，通常有kruskal算法和prim算法2种解。

  参考资料1  

  参考资料2 

 这里我用的是kruskal算法算法来解的，并通过并查集来将这个算法简化。

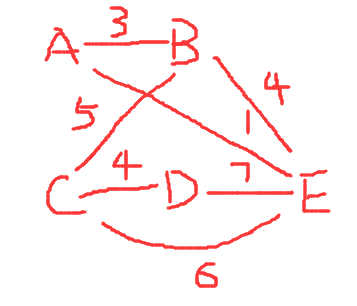
瞎jb画的，随便看看

from operator import itemgetter

class DisjointSet():
    '并查集，并查集通常用来解决非常多的元素的集合归属问题，是一种树形结构，因为每个node只需要记录自己的根node，所以在python中也可以简化成字典'
    forest = {}

    def add(self,list):
        for i in list:
            self.forest[i]=i

    def find(self,key):
        if self.forest[key]!=key:
            return self.find(self.forest[key])
        else:
            return key

    def union(self,key1,key2):
        self.forest[key2] = key1
        # print(self.forest)

if __name__ == '__main__':
    '主函数'
    nodes = ['a','b','c','d','e']
    forest = DisjointSet()
    forest.add(nodes)

    # 求最小生成树 有权重无向
    graph_list = [
        ('a','e',1),
        ('a', 'b', 3),
        ('b', 'e', 4),
        ('b', 'c', 5),
        ('c', 'd', 2),
        ('c', 'e', 6),
        ('d', 'e', 7)
    ]

    # 最小生成树
    print('最小生成树为：')
    for i in sorted(graph_list,key=itemgetter(2)):
        if forest.find(i[0])!=forest.find(i[1]):
            print(i)
            forest.union(i[0],i[1])

最小生成树 kruskal 图结构 路线问题